Superficies en el espacio

¿las funciones vectoriales ?¿superficies en el espacio?

las funciones vectoriales  representan superficies en el espacio

Una curva en el espacio también se representa en forma vectorial.

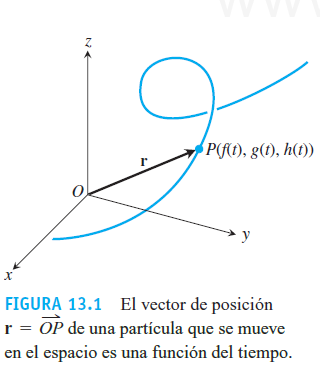
Las funciones f , g y h son las funciones componentes (los componentes) del vector de posición.

El vector del origen a la posición de la partícula P( f (t ), g(t ), h(t )) en el tiempo t es el vector de posición de la partícula

Consideramos la trayectoria de la partícula como la curva trazada por r durante el intervalo de tiempo I.

El significado geométrico de la definición de derivada

El significado geométrico de la definición de derivada de una función vectorial

Los puntos P y Q tienen vectores posición

el vectorPQ se representa mediante 

apunta en la misma dirección

que el vector PQ.

Definición de Derivadas de función Vectorial

Referencia  bibliográfica de algunas definiciones de derivadas de Funciones Vectoriales

 Una función vectorial r es derivable si es derivable en cada punto de su dominio. La curva
trazada por r es suave (regular) si dr/dt es continua y nunca es 0, es decir, si f , g y h tienen
primeras derivadas continuas y éstas no se anulan en forma simultánea
Según el autor del libro : Thomas-Calculo-Varias-Variables-12-Edicion

Según el libro:Calculo Leithold 7Ed